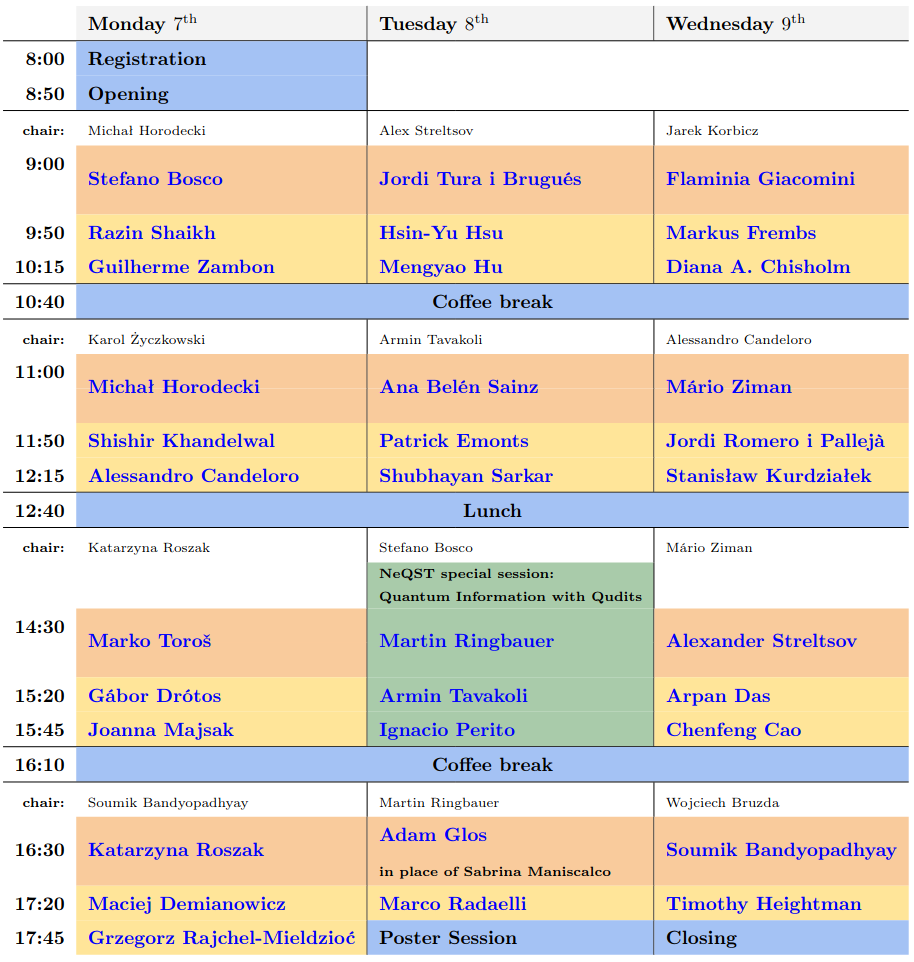
About the conference
Quantum Information is a rapidly developing field, attracting a large number of researchers, and leading to exciting fundamental discoveries and practical applications. The main aim of the Quantum Information Days 2024 (QID2024) workshop is to bring together young researchers working on widely understood quantum information sciences and related fields. We hope to inspire vivid scientific discussions and foster new collaborations. Young researchers will have the possibility of presenting their recent results in the form of a talk (approx. 20 minutes long) or a poster. A number of invited talks by recognized scientists is also planned. The meeting will be held in Warsaw, Poland, a lively Central European city with rich cultural and urban life.
This is a second edition of the workshop Quantum Information Days 2020(+1) (qid2020.cft.edu.pl), which was held fully online due to the coronavirus pandemic.
The conference fee is 100€ (450 zł).
Participants from CFT (employees and PhD students) do not have to cover the fee.
Please contact us at qid2024@cft.edu.pl in case you need any assistance.
Warning!
We have confirmed email scams targeting participants of QID 2024. Please ignore emails from "ops@travellerpoint dot net", or any other travel agency. Do not reply to the emails and do not click any links included in these emails.